[Nächstes Kapitel] [vorangehendes Kapitel] [vorangehendes Kapitel (SeitenEnde)] [SeitenEnde] [Inhalt]
Melden Sie sich auf der Startseite www.eAssistant.eu mit Ihrem Benutzernamen und Ihrem Passwort an. Um das Berechnungsmodul für spiralverzahnte Kegelräder zu starten, klicken Sie in der Baumstruktur auf der linken Seite auf den Menüpunkt „Zahnradberechnung“ und anschließend auf „Spiral-Kegelräder“.

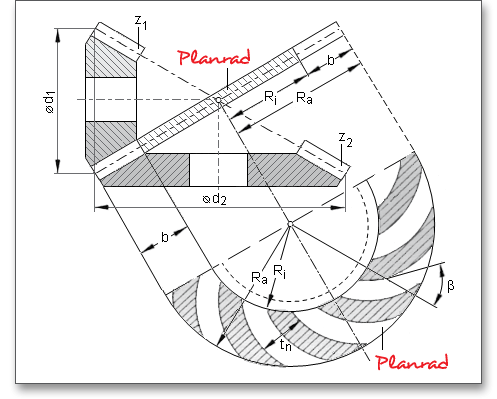
Die generelle Berechnung der Geometrie von Kegelrädern erfolgt nach ISO 23509. Die Verzahnung eines Kegelrades ist durch den Teilkegelwinkel \(\delta \) und die dazugehörige Planradverzahnung eindeutig festgelegt. Das Planrad stellt eine senkrecht zur Achse stehende ebene Zahnscheibe dar, die identisch ist mit einem Kegelrad mit einem Teilkegelwinkel von 90\(^{\circ }\). Für das Bezugsprofil ist die Planradverzahnung maßgebend. Die Beziehung von Planrad und Kegelrad ist vergleichbar mit der von Zahnstange und Stirnrad.
In dem Konfigurationsbereich des Berechnungsmoduls starten Sie mit der Vorgabe des Eingriffswinkels, der
Zähnezahlen und einem gewünschten Teilkegeldurchmesser am Rückenkegel des Tellerrades. Es werden Ihnen
anschließend entsprechende Vorschläge für den empfohlenen Wertebereich für Zahnbreite, Modul und
Spiralwinkel angezeigt.
Hinweis: Die Ergebnisse werden während jeder Eingabe berechnet und immer aktuell im Ergebnisfeld
angezeigt. Es wird nach jeder abgeschlossenen Eingabe neu durchgerechnet. Grundsätzlich können Sie jede
Eingabe mit der Enter-Taste oder mit einem Klick in ein neues Eingabefeld abschließen. Alternativ können
Sie mit der Tab-Taste durch die Eingabemaske springen oder nach jeder Eingabe auf den Button
„Berechnen“ klicken. Auch hierbei werden die Werte entsprechend übernommen und die Ergebnisse sofort in
der Übersicht angezeigt.
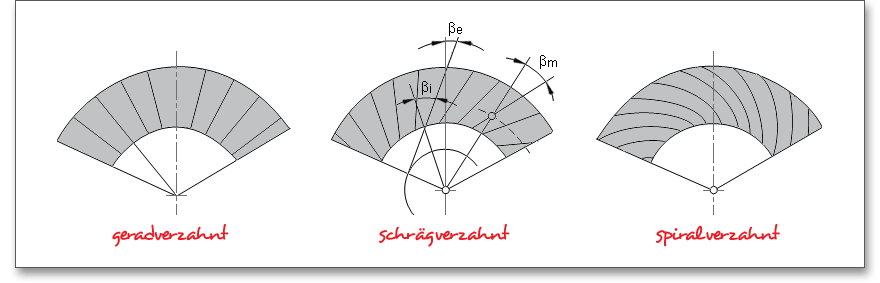
Es gibt verschiedene Arten von Kegelrädern, die sich zum Beispiel nach dem Verlauf der Zahnhöhe entlang der Zahnbreite oder der Art der Flankenlängslinie unterscheiden. Der Form der Flankenlinie entsprechend unterscheidet man gerad-, schräg- und spiralverzahnte Kegelräder.
Bei den Klingelnberg-Spiralkegelräder unterscheidet man zwei Herstellungsverfahren und deshalb auch zwei Verzahnungsarten, gekennzeichnet durch Palloid® und Zyklo-Palloid®. Die eAssistant-Software ermöglicht die einfache und schnelle Berechnung der Geometrie von Klingelnberg Zyklo-Palloid®-Spiralkegelrädern. Palloid®-Spiralkegelräder werden mit schneckenförmigen Fräsern verzahnt, Zyklo-Palloid®-Spiralkegelräder dagegen mit einem Messerkopf. Vorteile von Zyklo-Palloid®-Verzahnungen sind zum Beispiel:
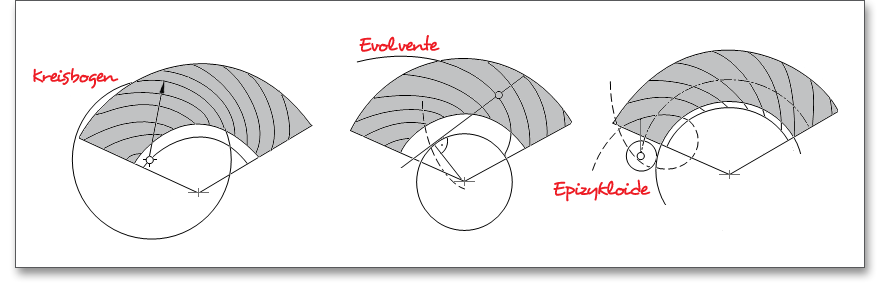
Der Verlauf der Zahnflanke zur Kegelspitze wird durch die Form der Leitlinie bestimmt. Hierbei lassen sich Kreisbogen, verlängerte Epizykloide und Evolvente unterscheiden.
Eine Zyklo-Palloid®-Verzahnung besitzt als Flankenlinie eine verlängerte Epizykloide. Jeder Punkt eines
Kreises, der auf einem fest stehenden Kreis rollt, beschreibt eine Epizykloide. Zyklo-Palloid®-Verzahnungen,
ursprünglich entwickelt für kleinere Räder, verfügen außerdem eine über der Zahnbreite konstanten Zahnhöhe.
Wenn der Kegelradzahn über der Zahnbreite eine konstante Zahnhöhe aufweist, müssen der Kopf- und
Fußkegelwinkel gleich groß sein und beide haben ohne eine Winkelkorrektur den gleichen Wert wie der
Teilkegelwinkel. Die Zahnkopflinie verläuft somit parallel zur Zahnfußlinie. Wenn die Zahnköpfe der Zehe dünner
werden als der zulässige Wert, bei dem ein Durchhärten am Zahnkopf beginnt, wird eine Kopfkürzung
durchgeführt.
Hinweis: Die eAssistant-Software prüft, ob eine Kopfkürzung notwendig ist und führt diese auch
automatisch aus, um das Durchhärten zu vermeiden. Die Kopfkürzung kann auch manuell beeinflusst
werden.
Die Kopf- und Fußkegelwinkel sind gleich groß, so dass die Zahnhöhe über die Zahnbreite konstant bleibt. Ohne eine Winkelkorrektur haben Kopf- und Fußkegelwinkel den gleichen Wert wie der Teilkegelwinkel. Die Zahnkopflinie verläuft parallel zur Zahnfußlinie.
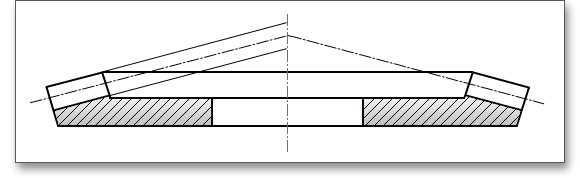
Bei dem Zyklo-Palloid®-Verfahren ist der Eingriffswinkel werkzeugbedingt in 17,5\(^{\circ }\) und 20\(^{\circ }\) vorgegeben. 20\(^{\circ }\) hat sich als ein günstiger Wert für den Eingriffswinkel herausgestellt. Öffnen Sie das Berechnungsmodul, ist standardmäßig ein Eingriffswinkel von 20\(^{\circ }\) eingestellt. Als maximalen Wert können Sie 45\(^{\circ }\) eingeben.
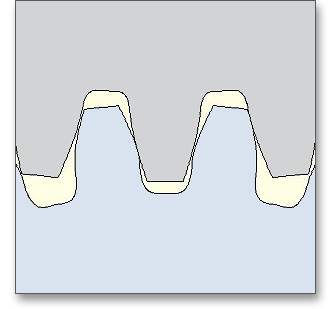
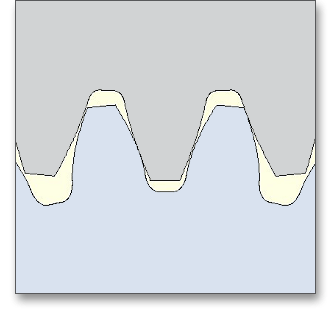
Am Beispiel eines Stirnrades wurde für a), b) und c) die Zahnform mit sonst identischen Parametern berechnet:
Der Achswinkel \(\Sigma \) eines Kegelradpaares ist der Winkel zwischen den beiden Radachsen, der dem Zahneingriff
zugewandt ist. Der Achswinkel kann zwischen 0\(^{\circ }\) und 180\(^{\circ }\) betragen. Vorzugsweise wird in den meisten
Anwendungsfällen ein Achswinkel von 90\(^{\circ }\) eingesetzt.
Kegelräder kann man hinsichtlich des Achsversatzes unterscheiden. Die Achsen der Kegelräder
können sich kreuzen oder schneiden. Kegelräder ohne Achsversatz besitzen sich schneidende
Achsen, bei Kegelrädern mit Achsversatz kreuzen sich die beiden Radachsen. Die Kegelräder werden
dann Hypoidräder genannt. Nachfolgend werden nur Kegelräder ohne Achsversatz betrachtet, also
\( a = 0\).
Die Zähnezahl hat Einfluss auf die Profilkrümmung, Zahnhöhe und Herstellbarkeit der Verzahnung (z.B. Unterschnitt, spitze Zähne). Bei der Wahl der Zähnezahl sollten Sie berücksichtigen, dass die kleinste zulässige Zähnezahl „5“ beträgt, doch um gute Laufeigenschaften zu erzielen, sollten Sie Werte über „8“ wählen.
Die Zähnezahl „5“ ist die kleinste Zähnezahl, die Sie in das Eingabefeld eintragen können. Das Ritzel erhält immer die kleinere Zähnezahl. Die ISO 23509 (für Spiralkegelräder und Hypoidkegelräder) enthält Vorschläge für die Wahl der Mindestzähnezahlen des Ritzels in Abhängigkeit des Zähnezahlverhältnisses \(u = z_{2}/z_{1}\).
| Anhaltswerte für Mindestzähnezahlen des Ritzels1
| |
| Approximate Ratio | Minimum Number of Pinion Teeth, \(z_{1}\) |
| \(1,00 \leq u \leq 1,50\) | 13 |
| \(1,50 \leq u \leq 1,75\) | 12 |
| \(1,75 \leq u \leq 2,00\) | 11 |
| \(2,00 \leq u \leq 2,50\) | 10 |
| \(2,50 \leq u \leq 3,00\) | 9 |
| \(3,00 \leq u \leq 3,50\) | 9 |
| \(3,50 \leq u \leq 4,00\) | 9 |
| \(4,00 \leq u \leq 4,50\) | 8 |
| \(4,50 \leq u \leq 5,00\) | 7 |
| \(5,00 \leq u \leq 6,00\) | 6 |
| \(6,00 \leq u \leq 7,50\) | 5 |
| \(7,50 \leq u \leq 10,0\) | 5 |
| 1 ISO 23509: Bevel and Hypoid Gear Geometry, S. 70, Tabelle B.2
| |
Hinweis: Bei der Herstellung auf Klingelnbergmaschinen sollten die Zähnezahlen von Rad bzw.
Ritzel und die Messerkopfgangzahl möglichst keinen gemeinsamen Teiler haben, damit sich nicht
immer die gleichen Messer im Eingriff befinden. Sie erhalten einen entsprechenden Hinweis im
Meldungsfenster.
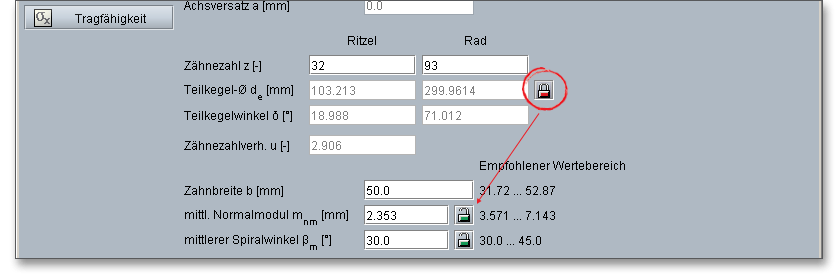
Der Teilkegeldurchmesser \(d_{e}\) ist der äußere Durchmesser des Teilkegels. Der Teilkegel ist die Bezugsfläche (Rotationsfläche um die Radachse) für ein Kegelrad, also nur eine gedachte Fläche, auf welche die geometrischen Bestimmungsgrößen bezogen werden. Der Teilkegelwinkel \(\delta \) ist der Winkel zwischen der Radachse und einer Teilkegel-Mantellinie. Neben dem Teilkegelduchmesser befindet sich ein Schloss-Button, der je nach Vorgabe aktiviert oder deaktiviert ist. Mit einem Klick auf den Schloss-Button lässt sich dieser umschalten. Mit dem Verriegeln des Eingabefeldes für den Teilkegeldurchmesser wird parallel das Eingabefeld für den Normalmodul freigeschaltet. Somit besteht die Möglichkeit, den Normalmodul und den Spiralwinkel gleichzeitig zu modifizieren. Ein Klick auf den Schloss-Button von Normalmodul oder Spiralwinkel genügt, um das Eingabefeld für den Teilkegeldurchmesser zu aktivieren.
Definiert ist die Zahnbreite \(b\) als Abschnitt einer Teilkegelmantellinie zwischen der äußeren und der inneren Endfläche der Zähne.
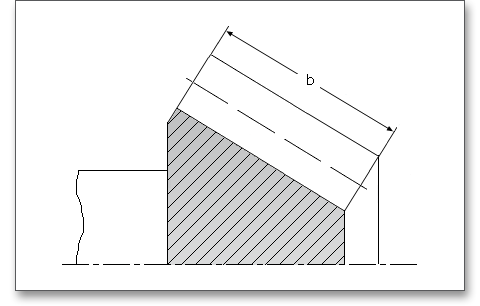
Die Zahnbreite ist vom Verwendungszweck des Getriebes und der äußeren Teilkegellänge \(R_{e}\) abhängig. Die folgende Übersicht beinhaltet einige Anhaltswerte:
| Anhaltswerte für die Wahl der Zahnbreite \(b\)2
| |
| Verwendungszweck | Zahnbreite \(b\) |
| Leicht und mittelschwer beanspruchte Getriebe für Maschinen und Fahrzeuge | \(3,5 \leq (R_{e}/b) \leq 5,0\) |
| Hochbeanspruchte Getriebe für Maschine, Straßen- und Schienenfahrzeuge | \(3,0 \leq (R_{e}/b) \leq 3,5\) |
| 2 Klingelnberg KN3028: Auslegung eines Kegelradgetriebes ohne Achsversatz mit
Klingelnberg Zyklo-Palloid®-Verzahnung, S. 11
| |
Der Normalmodul \(m_{n}\) (Verhältnis von Teilkegeldurchmesser zu Zähnezahl) ist die Basisgröße für die Längenmaße einer Kegelradverzahnnung und wird für eine bestimmte Teilkegellänge angegeben. Der Normalmodul an der mittleren Teilkegellänge \(R_{m}\) ist als Nenngröße recht gebräuchlich. Der Normalmodul wird nach der Eingabe aus dem mittleren Spiralwinkel berechnet. Hinter dem Eingabefeld erhalten Sie vom Berechnungsmodul einen Wertebereich vorgeschlagen, in dessen Grenzen Sie sich mit Ihren Eingabewerten bewegen sollten. Ist das Eingabefeld für den Normalmodul deaktiviert, können Sie das Eingabefeld über die Schloss-Funktion freischalten, um den Normalmodul leicht zu modifizieren.
| Anhaltswerte für die Wahl des Normalmoduls \(m_{n}\)3
| |
| Verwendungszweck | Normalmodul \(m_{n}\) |
| Oberflächengehärtete, zahnbruchgefährdete Spiralkegelräder | \(7 \leq (b/m_{n}) \leq 10 ... (12)\) |
| Pittinggefährdete oder vergütete und ungehärtete Spiralkegelräder | \(10 \leq (b/m_{n}) \leq 12 ... (14)\) |
| 3 Klingelnberg KN3028: Auslegung eines Kegelradgetriebes ohne Achsversatz mit Klingelnberg
Zyklo-Palloid®-Verzahnung, S. 12
| |
Der Spiralwinkel \(\beta \) ist der spitze Winkel der Tangente an der Teilflankenlinie und der Teilkegel-Mantellinie im
Berührpunkt der Tangente. \(\beta _{m}\) ist der Winkel an der mittleren Teilkegellänge. Bei Bogenverzahnungen verändert
sich der Spiralwinkel über der Zahnbreite kontinuierlich. Der Winkel kann beliebig gewählt werden.
Für ein optimales Laufverhalten von Zyklo-Palloid®-Kegelrädern sollte ein Spiralwinkel \(\beta _{m}\) von 30\(^{\circ }\)
bis 45\(^{\circ }\) gewählt werden. Der Spiralwinkel hat Einfluss auf die Überdeckung, die Zahnkräfte sowie
Lagerbelastungen. Auch das Eingabefeld für den Spiralwinkel besitzt eine Schloss-Funktion mit der Sie
die Eingabe manuell beeinflussen können. Da sich Zahnbreite, Normalmodul und Spiralwinkel
gegenseitig beeinflussen, können Sie die Werte solange verändern, bis diese Ihren Vorstellungen
entsprechen.
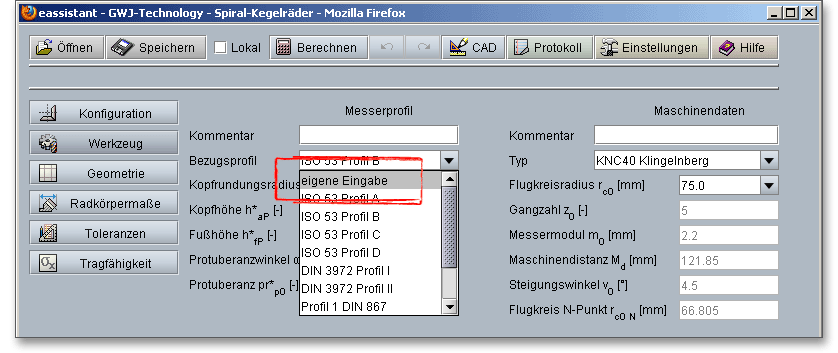
Hier können Sie aus einer Liste ein vordefiniertes Bezugsprofil wählen oder auch individuell vorgeben. Firmenspezifische Werkzeuge können über „Eigene Eingabe“ eingegeben werden. Die Maschinenauswahlliste zeigt, welche Klingelnbergmaschinen für die Herstellbarkeit einsetzbar sind. Individuelle Maschinendaten oder Maschinendaten nach ISO können ebenfalls festgelegt werden.
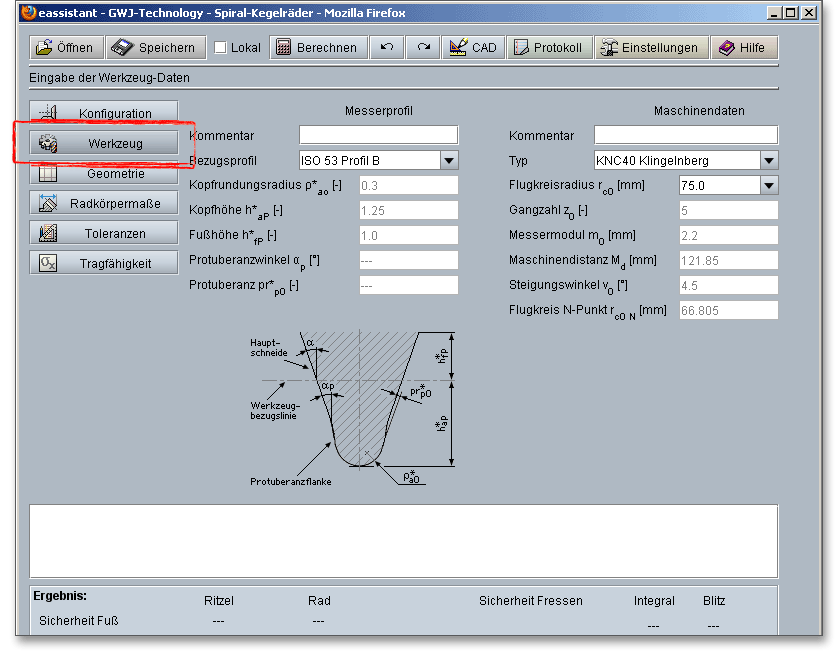
Hinweis: Ergänzen Sie in der Kommentarzeile eine kurze Notiz oder eine Anmerkung zum Messerprofil bzw. zu
den Maschinendaten. Die Bemerkung erscheint später auch im Protokoll.
Das Zyklo-Palloid®-Verfahren ist ein kontinuierlich arbeitendes Verfahren, bei dem für das Fräsen der rechten
und linken Zahnflanken des Kegelrads ein zwei geteilter Messerkopf eingesetzt wird. Der benutzte Messerkopf
entspricht einer Spiralplanschnecke, deren Messer sich in den zu schneidenden Lücken verschrauben. Der
Messerkopf besteht aus zwei ineinandergreifenden Teilen, ein innenschneidender Teil für die erhabenen
Flanken (konvexe Flanken) und ein außenschneidender Teil für die hohlen Flanken (konkave Flanken). Die
Hauptmesser sind zu einer Messergruppe zusammengefasst. Je nach Zahl der Messergruppen
werden ein- oder mehrgängige Messerköpfe unterschieden. Rechts- und linksspiralige Räder (Rad
und Ritzel eines Räderpaares) können mit dem gleichen Messerkopf verzahnt werden, nur die
Messer der einen Spiralrichtung müssen gegen die der anderen Spiralrichtung ausgewechselt
werden. Der Vorteil des geteilten Messerkopfes besteht darin, dass man den Flankenleitlinien von
Rad und Gegenrad sehr genau unterschiedliche Krümmungen geben kann und so jede Balligkeit
erreicht.
Als Bezugsprofil von Zyklo-Palloid®-Spiralkegelrädern ist das Normalschnittprofil des Planrades am mittleren Radius \(R_{m}\) definiert. Es entspricht im allgemeinen dem Bezugsprofil von Stirnrädern nach DIN 867. Abweichend von der DIN 867 wird auch ein Bezugsprofil mit Zahndickenänderung verwendet. Die Zahndicke auf der Profilbezugslinie ist dann nicht mehr gleich der Zahnlücke, sondern um einen Betrag von \(2 \cdot x_{s} \cdot m_{n}\) verschieden. Die folgenden genormten Bezugsprofile stehen Ihnen für die Berechnung zur Verfügung und können über eine Listbox ausgewählt werden:
Hinweis: Wenn Sie in der Listbox „Eigene Eingabe“ wählen, werden der Kopfrundungsradius, die Kopfhöhe und die Fußhöhe aktiviert. Sie können so schnell das Bezugsprofil individuell vorgeben.
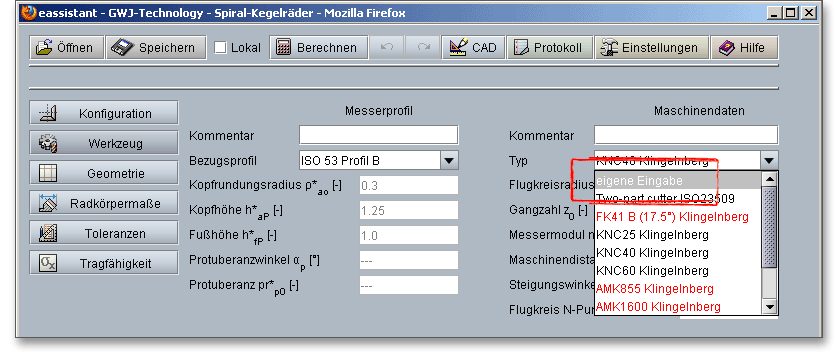
Der eAssistant bietet eine Auswahl an verschiedenen Maschinentypen. Die folgenden Maschinentypen stehen in einer Listbox zur Auswahl bereit:
Hinweis: Wählen Sie in der Listbox „Eigene Eingabe“, dann werden der Flugkreisradius, die Gangzahl und der Messermodul aktiviert. So können Sie auch hier schnell individuelle Maschinendaten vorgeben.
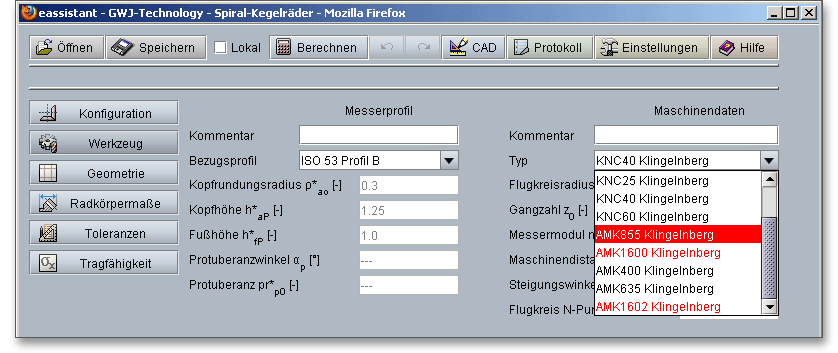
Bei der Vielzahl der Maschinen zeigt das Berechnungsmodul Ihnen automatisch an, welcher Maschinentyp für die Herstellung eingesetzt werden kann. Die Maschinentypen, die ungeeignet für den entsprechenden Anwendungsbereich sind, werden rot gekennzeichnet. Wenn Sie eine Maschine auswählen, werden sofort die möglichen Flugkreise ermittelt.
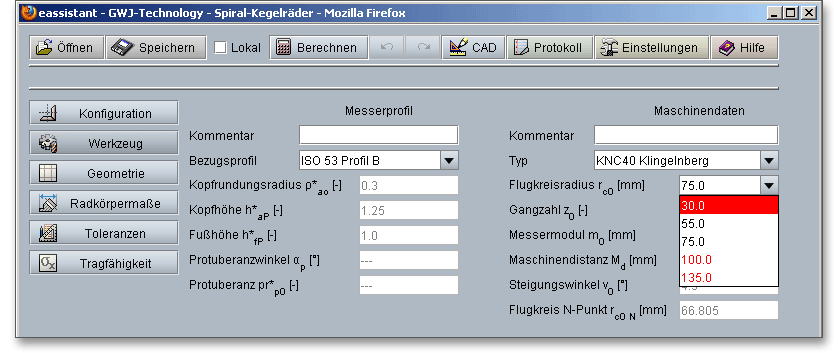
Der Flugkreisradius ist der Abstand der profilgebenden Schneide von der Rotationsachse des Messerkopfes. Der Flugkreisradius bestimmt den Krümmungsradius der Flankenlängslinie und hat dadurch einen großen Einfluss auf das Verlagerungsverhalten der Kegelradverzahnung. Weiterhin ergibt sich ein Einfluss auf die inneren und äußeren Spiralwinkel der Verzahnung und auf den Verlauf der Zahnlückenweite im Normalschnitt entlang der Zahnbreite.

Der Flugkreisradius beschränkt sich aus wirtschaftlichen Gründen auf genormte Standardwerte, die in einer Listbox zur Auswahl stehen. Die Flugkreise, die nicht in Frage kommen, werden rot markiert. So lässt sich schnell erkennen, welche Flugkreise möglich sind. Bei dem Maschinentyp „Eigene Eingabe“ können Sie eine individuelle Vorgabe des Flugkreisradiuses vornehmen.
Das Zyklo-Palloid®-Verfahren ist ein kontinuierliches Verfahren, bei dem die Messer zu Messergruppen zusammengefasst sind, wobei nur eine Messergruppe jeweils eine Zahnlücke bearbeitet. Die Anzahl der Messergruppen wird als Gangzahl \(z_{0}\) bezeichnet. Die Maschinendistanz \(M_{d}\), der Radius des Messerkopfmittelpunkts, wird automatisch berechnet und angezeigt.
In der Geometriemaske des Berechnungsmoduls erfolgt die Vorgabe der Spiralrichtung sowie der Profilhöhen- und Profilseitenverschiebung.
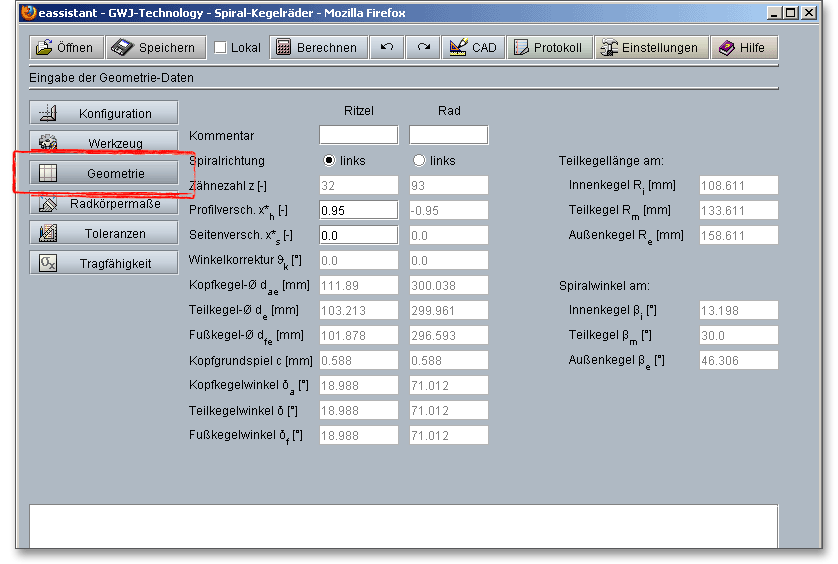
Zu einem linksspiraligen Ritzel gehört ein rechtspiraliges Tellerrad und umgekehrt. Schaut man von der Spitze des Teilkegels aus auf den aufrecht stehenden Zahn und der Zahn verläuft nach rechts, dann ist eine Verzahnung rechtssteigend bzw. linkssteigend, wenn der Zahn nach links verläuft. Ist die Spiralrichtung für das Ritzel festgelegt, ergibt sich für das Tellerrad die entgegengesetzte Richtung. Die Gängigkeit des gesamten Kegelradgetriebes wird nach der Gängigkeit des Ritzels bezeichnet. Zwischen beiden Spiralrichtungen besteht hinsichtlich des Geräuschverhaltens sowie des Wirkungsgrades kein Unterschied.

Kegelradverzahnungen werden immer als „V-Null-Verzahnung“ ausgelegt. Das bedeutet, dass
stets ein Kegelrad mit einer positiven Profilverschiebung mit einem Kegelrad mit gleich großer
negativer Profilverschiebung gepaart wird. Die Summe der Profilverschiebungen beträgt daher
„0“.
Die Profilverschiebung ist
Die folgenden Faktoren spielen bei der Wahl der Profilverschiebung eine maßgebende Rolle:
Bei der Profilseitenverschiebung sind die Flanken des Bezugsprofils seitlich verschoben. Die Zahnfußdicke wird
verändert und damit ändert sich auch die Zahnlückenweite. Die Profilseitenverschiebung kann frei gewählt
werden und wird genutzt, um die unterschiedliche Zahnfußtragfähigkeit am Tellerrad und Ritzel auszugleichen.
Betragsmäßig ist \(x_{S}^{\ast }\) am Ritzel und Rad gleich groß. Mit der Profilseitenverschiebung ist eine vielseitige
Korrekturmöglichkeit gegegeben.
Eine Winkelkorrektur wird durchgeführt, um am kleinen Durchmesser \(R_{i}\) eine zusätzliche Profilverschiebung für das Ritzel zu schaffen und somit ein Einschneiden des Messerkopfes in nebenstehende Zapfen zu verhindern. Allgemein sollte die Winkelkorrektur einen Betrag von 5\(^{\circ }\) nicht übersteigen und sollte auch nur bei bestimmten Sonderfällen eingesetzt werden. Diese Funktion ist im eAssistant noch nicht verfügbar.
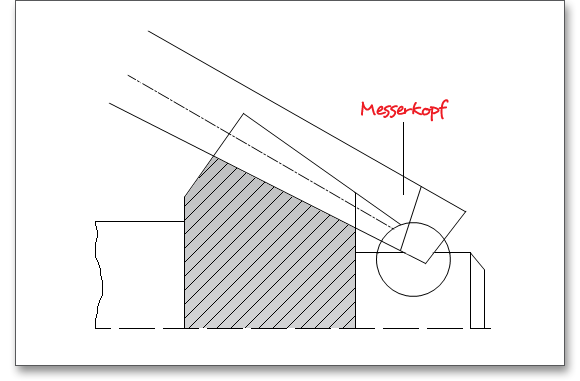
Das Kopfgrundspiel \(c\) ist der minimale Abstand zwischen dem Zahnkopf und dem Zahngrund des Gegenrades. Die Größe des Kopfgrundspiels beträgt standardmäßig 0,25 mal mittlerem Normalmodul.
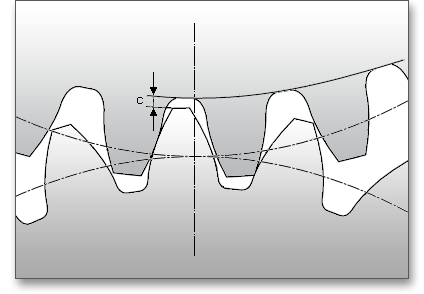
Der Kopfkegelwinkel ist der von der Radachse und der Kopfkegel-Mantellinie eingeschlossene
Winkel.
Der Fußkegelwinkel ist der von der Radachse und der Fußkegel-Mantellinie eingeschlossene Winkel.
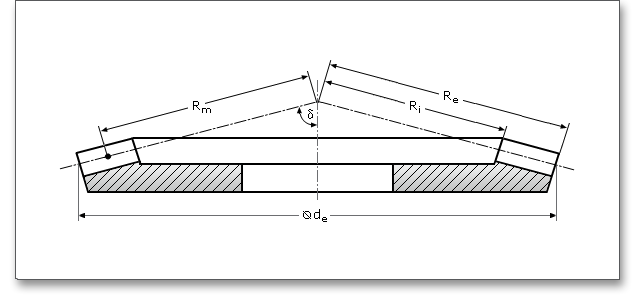
Die Teilkegellänge \(R\) ist der Spitzenabstand auf dem Teilkegel. Die mittlere Teilkegellänge \(R_{m}\) bezeichnet die Länge der Mantellinien des vom mittleren Teilkegeldurchmessers begrenzten Teilkegels oder die um die halbe Zahnbreite \(b\) verminderte äußere Teilkegellänge. Die innere Teilkegellänge \(R_{i}\) ist die Länge der Mantellinien des vom inneren Teilkegeldurchmessers begrenzten Teilkegels oder die um die Zahnbreite \(b\) verminderte äußere Teilkegellänge. Die äußere Teilkegellänge \(R_{e}\) ist die Länge der Mantellinien des vom äußeren Teilkegeldurchmessers begrenzten Teilkegels.
In dieser Eingabemaske werden alle Radkörpermaße ergänzt, so dass diese für eine spätere Zeichnung oder für ein CAD-Modell genutzt werden können. Für den Fall, dass eine Kopfkürzung notwendig ist, wird diese hier automatisch ausgeführt. Die Kopfkürzung kann jedoch auch über den Button „Kopfkürzung“ ganz einfach manuell beeinflusst werden.
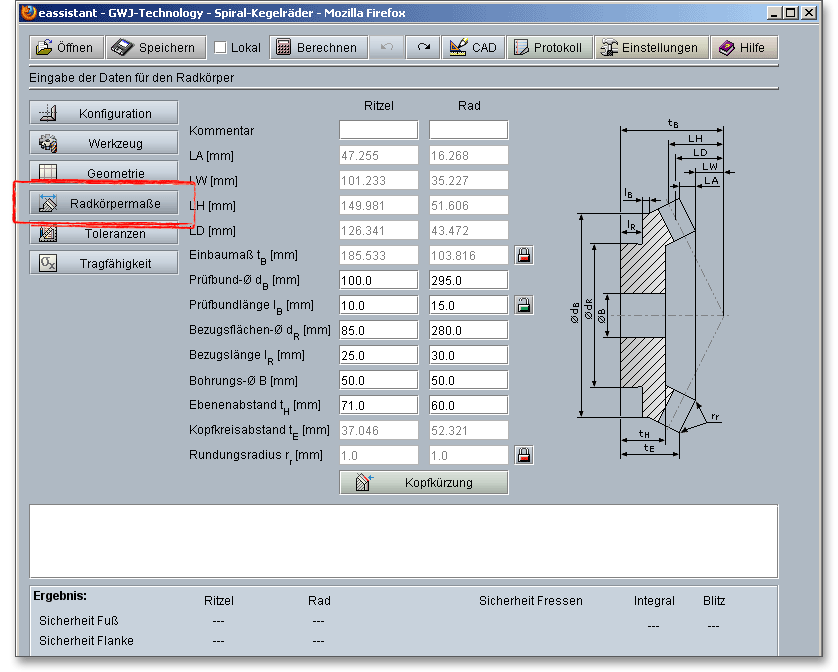
Das Einbaumaß \(t_{B}\) ist der Abstand zwischen Teilkegelspitze und Bezugs-Stirnfläche. Diese Länge wird als
Bezugsmaß für die Herstellung, Prüfung und den Einbau des Kegelrades benötigt. Neben dem Einbaumaß
befindet sich ein Schloss-Button, der standardmäßig deaktiviert ist. Mit einem Klick auf den Schloss-Button
kann dieser aktiviert werden, um einen individuellen Wert für das Einbaumaß einzugeben und somit das Maß
frei zu modifizieren. Ist die Eingabe für das Einbaumaß aktiviert, wird das Eingabefeld für die Prüfbundlänge
automatisch deaktiviert. Klicken Sie erneut auf den Schloss-Button, wird die Eingabe für die Prüfbundlänge
wieder freigeschaltet.
Der Hilfsebenenabstand \(t_{H}\) ist der Abstand zwischen der Bezugs-Stirnfläche und einer frei wählbaren, zur
Radachse senkrechten Hilfsebene.
Der Kopfkreisabstand \(t_{E}\) ist der Abstand zwischen dem Kopfkeis am Rückenkegel und der Bezugs-Stirnfläche.
Die Klingelnbergnorm KN 3028 gibt einige Anhaltswerte für den Rundungsradius \(r_{r}\) an den Zahnenden, die für Ritzel und Tellerrad gewählt werden können. Standardmäßig wird der Rundungsradius automatisch vom Berechnungsmodul gemäß der Klingelnbergnorm gesetzt. Klicken Sie den Schloss-Button an, um das Eingabefeld freizuschalten und um den Rundungsradius manuell anzupassen. Klicken Sie erneut auf den Button, wird der Wert automatisch wieder eingesetzt.

Die nachfolgenden Werte werden vom Berechnungsmodul automatisch gesetzt:
| \(m_{n}\) | 1,0-2,0 | 2,0-3,5 | 3,5-5,0 | 5,0-6,0 | 6,0-7,0 | 7,0-9,0 |
| \(r_{r}\) | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 |
| \(m_{n}\) | 9,0-10 | 10-13 | 13-14 | 14-16 | 16-19 | 19-25 |
| \(r_{r}\) | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 |
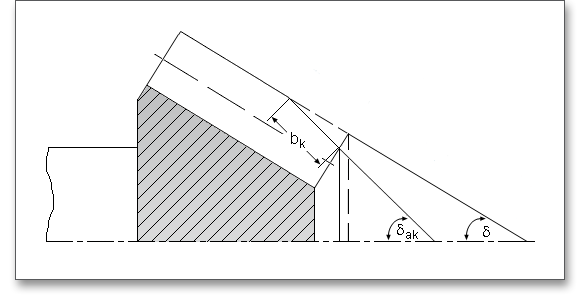
Wird an einem Kegelrad die Zahnkopfdicke \(s_{a}\) am Innenkegel kleiner als \(0,3 m_{n}\), so muss eine Kopfkürzung vorgenommen werden. Dadurch soll ein Durchhärten am Zahnkopf vermieden werden. Die Gefahr des spitzen Zahnes ist am kleinen Durchmesser des Ritzels am größten. Bei der Kopfkürzung wird über die Breite \(b_{k}\) der Kopfkegelwinkel auf \(\delta _{ak}\) vergrößert, so dass sich in diesem Bereich eine annähernd konstante Zahnkopfdicke von \(0,3 m_{n}\) einstellt.
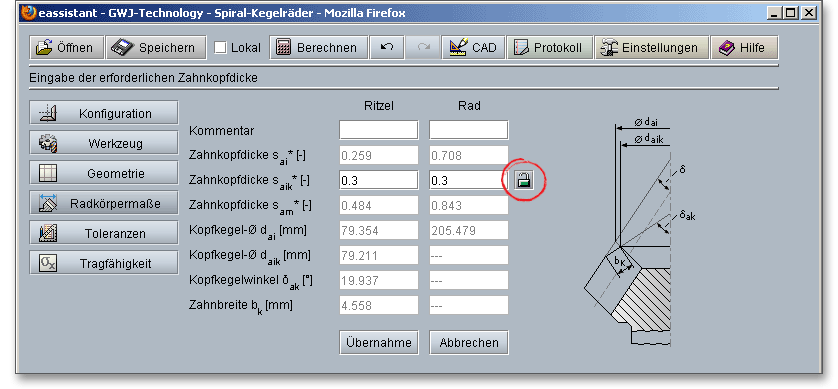
Das Berechnungsmodul führt die Kopfkürzung automatisch durch. Sie erhalten einen entsprechenden Hinweis im Meldungsfenster. Wenn Sie auf den Button „Kopfkürzung“ klicken, dann werden Ihnen die Werte für die Kopfkürzung angezeigt. Über den Schloss-Button können Sie die Zahnkopfdicke \(s_{aik}\) manuell festlegen und die Kopfkürzung somit beeinflussen. Klicken Sie erneut auf den Button, so wird der ursprüngliche Wert wieder eingesetzt.
Neben der Achslagengenauigkeitsklasse erhalten Sie hier Vorschläge für die Flankenspiele nach Klingelnberg oder Niemann. Eine individuelle Vorgabe eines Flankenspiels ist ebenfalls möglich.
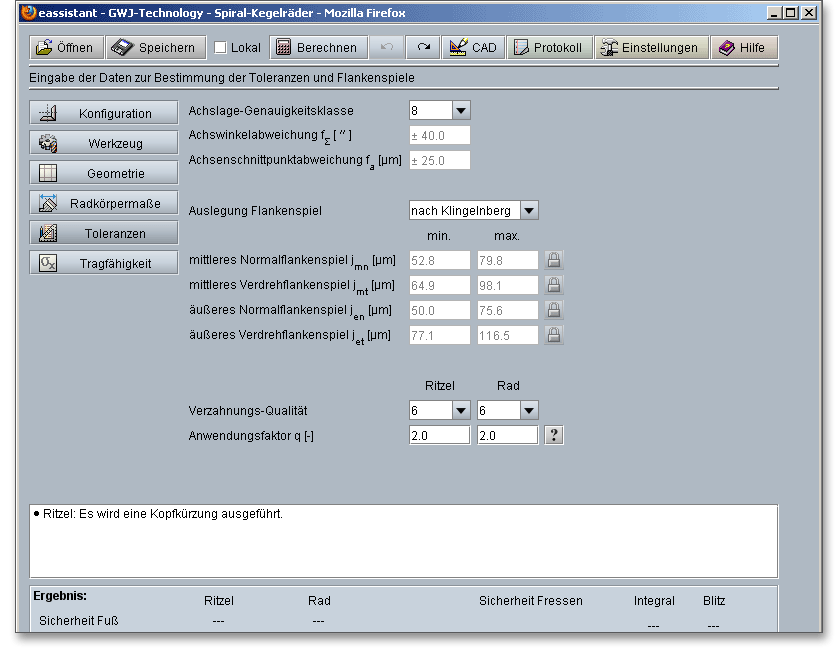
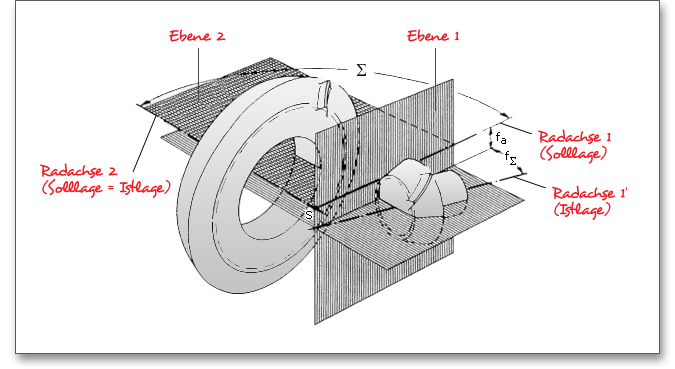
Die Achswinkelabweichung \(f_{\Sigma }\) ist der Unterschied zwischen dem Achswinkel der beiden Radachsen in ihren Ist-Lagen und dem Sollwert dieses Winkels. Die Achsenschnittpunktsabweichung \(f_{a}\) eines Kegelradpaares ist der Kreuzungsabstand der beiden Radachsen in ihren Ist-Lagen. Aus der Achslage-Genauigkeitsklasse ergeben sich die Achswinkelabweichung und Achsenschnittpunktsabweichung. Die Berechnung erfolgt nach DIN 3965.
Um ein Klemmen der Verzahnung und um Herstellungs- oder Einbauungenauigkeiten zu vermeiden, ist ein
Flankenspiel notwendig. Dabei muss ein definiertes für den Lauf erforderliches und günstiges Flankenspiel
sichergestellt werden.
Da Verzahnungen in der Praxis nicht frei von Abweichungen hergestellt werden können, soll das
Verdrehflankenspiels helfen, ein Klemmen oder Eingriffsstörungen der Verzahnung zu vermeiden. Ein zu
geringes Verdrehflankenspiel kann ein Klemmen zur Folge haben, ein zu groß bemessenes schwächt die
Zahndicke. Die Größe muss in Abhängigkeit der Verzahnungsgröße, der Verzahnungsqualität sowie der
Anwendung gewählt werden.
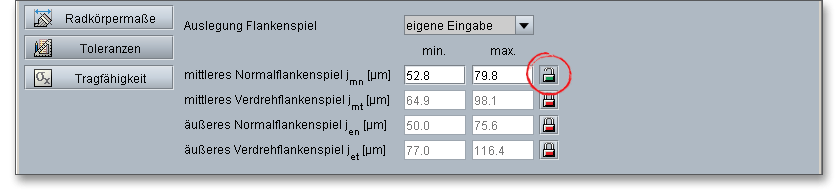
Das Normalflankenspiel und das Verdrehflankenspiel werden automatisch nach Klingelnberg oder Niemann berechnet. Die Methode für die Auslegung lässt sich aus der Listbox auswählen. Wenn Sie in der Listbox den Eintrag „eigene Eingabe“ wählen, können Sie ein individuelles Flankenspiel eingeben. Über den Schloss-Button lässt sich das entsprechende Eingabefeld freischalten und Sie können einen Wert festlegen. Wählen Sie wieder eine der vorgegebenen Methoden aus, werden der Schloss-Button und die Eingabefelder erneut deaktiviert.
Die ISO 17485 enthält zehn Verzahnungsqualitäten, von 2 bis 11. Die Qualität 2 bezeichnet dabei die beste Qualität, die Qualität 11 die geringste bzw. schlechteste Qualität.
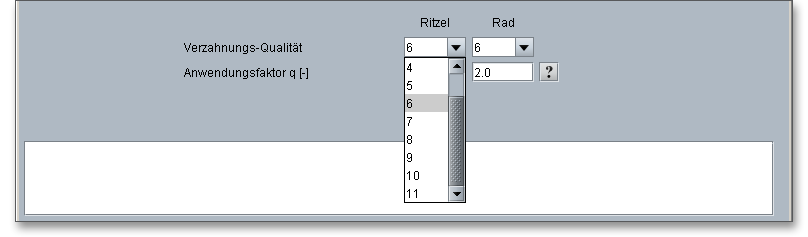
Durch die Verzahnungsqualität werden die folgenden zulässigen Toleranzen festgelegt:
Zur Ermittlung der zulässigen Toleranzen für eine vorgegebene Verzahnungsqualität wird nach ISO 17485 der Qualitäts-Anwendungsfaktor \(q\) benötigt. Um erhöhte Laufgeräusche oder Schäden wie Zahnbruch zu vermeiden, sollten die nachfolgenden Anhaltwerte für den Qualitäts-Anwendungsfaktor gemäß der ISO 17485 genutzt werden. Mit einem Klick auf den Fragezeichen-Button lässt sich die folgende Tabelle auch direkt im Berechnungsmodul aufrufen.

| Anhaltswerte für die Wahl des Anwendungsfaktors \(q\) nach ISO 174855
| ||
| Application | Typical Values for Amplitudes of Single Flank Composite Tooth Mesh Component Deviations | Factor \(q\) |
| Passenger car | < 30 | 0,05 |
| Truck | 20 - 50 | 1,0 |
| Industrial | 40 - 100 | 2 to 2,5 |
| Aircraft | 40 - 200 (80 average) | 2,0 |
| 5 ISO 17485: Bevel gears - ISO System of Accuracy, S. 26, Tabelle B.1
| ||
Bei der Berechnung der Tragfähigkeit geht es stets um den Nachweis der folgenden Festigkeitsfaktoren, die sich aus den genannten Schadensfällen ergeben:
Mit dem Modul können Sie die Zahnfuß-, Zahnflanken- sowie die Fresstragfähigkeit schnell und einfach überprüfen. Die Berechnung der Fresstragfähigkeit ist zur Zeit noch nicht verfügbar. Berücksichtigt werden die Materialeigenschaften, die Lebensdauer sowie die Schmierungsart und der entsprechend gewählte Schmierstoff. Die erweiterten Eingabeoptionen bieten die Möglichkeit, die Anzahl der Lastwechsel sowie die Rautiefe zu beeinflussen, die Betriebsart wird über den Betriebsartenfaktor gewählt.
Die folgenden Faktoren berücksichtigen die wesentlichsten Einflüsse bei der Tragfähigkeitsberechnung:
Die Zahnfußtragfähigkeit ist die durch die zulässige Zahnfußbeanspruchung bestimmte Tragfähigkeit. Ein
Zahnbruch kann zum Beispiel aus einer Schleifkerbe resultieren. Wird die Beanspruchung überschritten,
brechen die Zähne meist am Zahnfuß aus. Ein Zahnbruch zerstört die gesamte Verzahnung und führt somit
zum Ausfall eines Getriebes. Laut DIN 3990 ist nach einem Zahnbruch ein Betrieb mit verringerter Belastung
möglich, wenn nur ein kleiner Teil eines oder mehrerer Zähne ausgebrochen ist und die übrigen Teile der
Verzahnung unbeschädigt sind. Zahnbruch ist ein Ermüdungsschaden.
Günstig sind: positive Profilverschiebung (bei kleinen Zähnezahlen), Verwendung vergüteter oder gehärteter
Werkstoffe mit höherer Zahnfußfestigkeit, größere Zahnfußausrundung, größerer Modul, größerer
Eingriffswinkel, größere Zahnbreite
Die Grübchentragfähigkeit ist die durch die zulässige Flankenpressung bestimmte Tragfähigkeit.
Grübchenbildung ist ein Ermüdungsschaden. Bei einer Grübchenbildung entstehen an der Oberfläche feine
Risse, in die Öl eindringt. Beim Überrollen werden die Öffnungen verschlossen und Materialteilchen
herausgesprengt. Die Vertiefungen, die sich dadurch bilden, werden auch Grübchen (bzw. Pitting) genannt.
Diese Ausbröckelungen sind erst dann unzulässig, wenn die Anzahl der Grübchen zunimmt oder die Grübchen
größer werden. Grübchenfestigkeit ist ebenfalls ein Ermüdungsschaden.
Günstig sind: große Zähnezahl, positive Profilverschiebung (bei kleinen Zähnezahlen), größerer
Eingriffswinkel, hohe Flankenhärte, Nitrierhärten, zäheres Öl
Durch Mangel an Schmierstoff oder durch ein Zusammenbrechen des Schmierfilms können zwischen den Zahnflanken Verschleißerscheinungen auftreten. Diese Schadensform wird „Fressen“ genannt. Besonders bei mechanisch und thermisch hochbelasteten Verzahnungen tritt das Problem des Fressens auf. Infolge des Fressens steigen bei schnelllaufenden Getrieben die Temperatur, die Zahnkräfte sowie die Geräusche so stark an, dass der Schmierfilm zwischen den Zahnflanken abreißt. Die metallischen Flächen reiben aufeinander und es kommt zu kurzzeitigen örtlichen Verschweißungen der Flanken. Schließlich kommt es wegen der starken Flankenschäden zum Zahnbruch. Im Gegensatz zum Zahnbruch und zur Grübchenbildung ist das Fressen kein Ermüdungsschaden. Fressen kann ganz plötzlich auftreten. Bereits eine einzige kurze Überlastung kann zu einem Fressschaden führen und somit zum Ausfall der Zahnräder. Die Gefahr des Auftretens von Fressschäden wird beeinflusst von:
Nach dem Auftreten eines Fressschadens neigen schnelllaufende Getriebe zu hohen dynamischen Zusatzkräften, die als Folge von Fressen gewöhnlich Grübchenbildung oder Zahnbruch verursachen. Die hohen Oberflächentemperaturen führen zum Zusammenbrechen des Schmierfilms. Fressen wird begünstigt durch:
Günstig sind: EP-Öle (Öle mit chemisch aktiven Zusätzen), geeignete Werkstoffauswahl, sorgfältiges Einlaufen
der Verzahnung, geringe Gleitgeschwindigkeit oder kleineren Modul
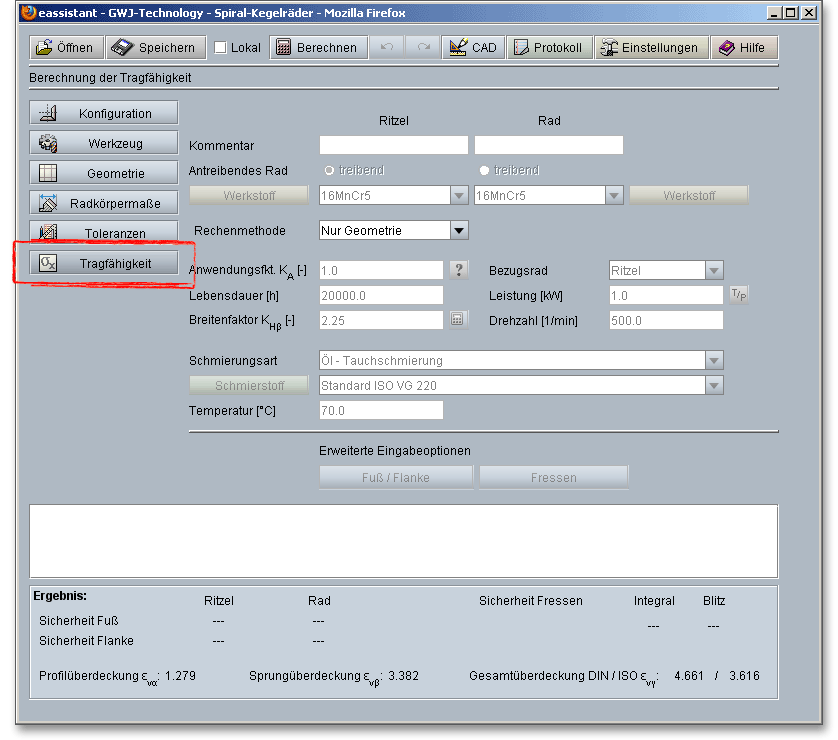
Wenn Sie auf den Button „Tragfähigkeit“ klicken, dann gelangen Sie in den Berechnungsbereich für die Tragfähigkeit. Sie werden bemerken, dass im Moment alle Eingabe- oder Auswahlfelder deaktiviert sind. Sobald Sie in der Listbox „Rechenmethode“ „ISO 10300 Methode B1“ auswählen, werden alle Eingabefelder aktiviert. Für den Fall, dass Sie die Tragfähigkeitsberechnung nicht benötigen, kann diese somit „ausgeschaltet“ werden. Dadurch verringert sich der Umfang des Protokolls.
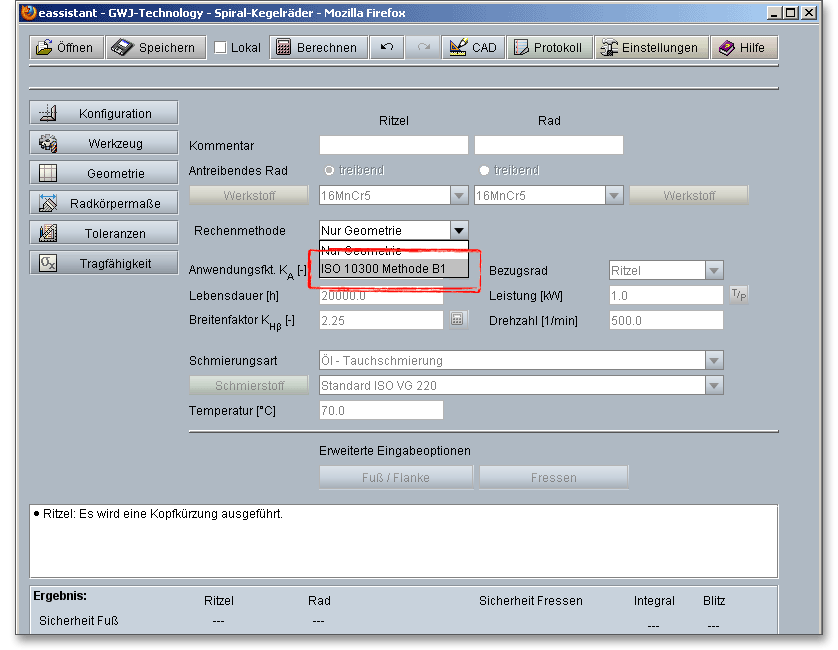
Ergänzen Sie in der Kommentarzeile eine kurze Notiz oder eine Anmerkung für Ritzel und Rad. Die Bemerkung erscheint später im Protokoll im Bereich der Tragfähigkeit.

Wählen Sie hier den entsprechenden Werkstoff für Ritzel und Rad direkt aus der Listbox oder klicken Sie auf den Button „Werkstoff“ über den Sie anschließend in die Werkstoffdatenbank gelangen.
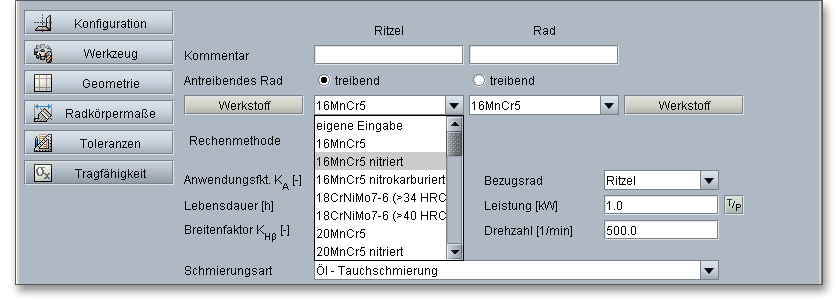
In der Werkstoffdatenbank erhalten Sie detaillierte Informationen zu den einzelnen Werkstoffen. Klicken Sie sich mit Hilfe der Cursor-Taste nach unten durch die Listbox. Somit lassen sich die einzelnen Werkstoffe anhand ihrer Eigenschaften miteinander vergleichen.
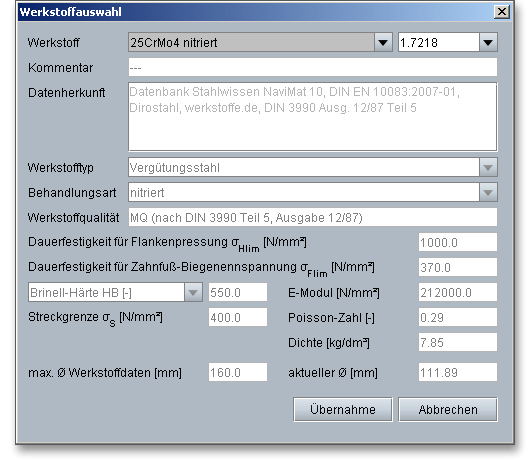
Für die Herstellung von Zahnrädern werden vorwiegend Stähle eingesetzt. Für Ritzel und Rad kann der gleiche
Vergütungsstahl eingesetzt werden. Bei der Werkstoffauswahl ist zu beachten, dass ungehärtete Räder gleicher
Härte nicht gepaart werden sollten, da hierbei große Neigung zum Fressen der Flanken besteht. Ein gehärtetes
oder nitriertes Rad \(HRC > 50\) glättet die Zahnflanken eines vergüteten Gegenrades, baut dessen Formabweichungen ab
und erhöht dadurch die Grübchentragfähigkeit. Bei einer Paarung gehärteter Räder sind keine
Härteunterschiede erforderlich.
Einsatzstahl: Hier handelt es sich um Qualitäts- und Edelstähle mit einem niedrigen Kohlenstoffgehalt. Sie
werden im Bereich der Randzone aufgekohlt, gegebenenfalls gleichzeitig aufgestickt und anschließend
gehärtet. Der Stahl hat nach dem Härten in der Randschicht eine hohe Härte und einen guten
Verschleißwiderstand, während der Kernwerkstoff vor allem eine hohe Zähigkeit aufweist.
Vergütungsstahl: Die entsprechenden Eigenschaften werden hier durch eine geeignete Wärmebehandlung
erreicht. Dies kann in Form einer Vergütung erfolgen. Vergüten bedeutet eine Wärmebehandlung von Stahl
durch Abschrecken aus Härtetemperatur und Anlassen auf so hohe Temperatur, dass die Zähigkeit wesentlich
gesteigert wird. Gleichzeitig wird eine höhere Elastizitätsgrenze erreicht. Die Anlasstemperaturen liegen
zwischen 400 bis 700\(^{\circ }\)C. Manche Stähle müssen nach dem Anlassen schnell abgekühlt werden
(Anlassen: Um notwendige Eigenschaften der Werkstücke, wie zum Beispiel gewünschte Festigkeit oder
Zähigkeit, zu erlangen, ist ein erneutes Erwärmen der Werkstücke auf bestimmte Temperaturen
notwendig.).
Stahl: Stahl wird am meisten für mittel- und hoch beanspruchte Zahnräder verwendet.
Stahlguss: Unter Stahlguss versteht man Eisenwerkstoffe mit C-Gehalten bis max. 2%, die in Formen aus Sand
zu Konstruktionsteilen vergossen werden. Infolge der höheren Schmelztemperatur ist Stahlguss
gegenüber Gusseisen schwer vergießbar. Stahlguss ist kostengünstiger als gewalzte oder geschmiedete
Räder.
Nitrierstahl: Bei diesem Stahl handelt es sich um Vergütungsstahl, der mit Cr, Mo und Ni legiert
ist.
Schwarzer Temperguss (perlitisches Gefüge): Teile mit komplizierter Form, die hohe Zähigkeit,
Schlagfestigkeit und gute Bearbeitung besitzen müssen, werden aus Temperguss hergestellt. Temperguss ist
für kleinere Abmessungen geeignet und besitzt gegenüber Stahlguss eine höhere Festig- und
Zähigkeit.
Gusseisen Kugelgraphit (perlitisches Gefüge, bainitisches Gefüge, ferritisches Gefüge): Unter Gusseisen
versteht man alle Eisen-Werkstoffe mit mehr als 2% C. Der maximale C-Gehalt liegt jedoch selten höher als
4.5%. Gusseisen ist ein sehr kostengünstiger Konstruktionswerkstoff, dessen Zähigkeit und Verformbarkeit
jedoch deutlich geringer sind als beispielsweise bei Stahl. Gusseisen mit Kugelgraphit ist für Teile mit höheren
Schwingbeanspruchungen geeignet.
Grauguss: Grauguss ist für komplizierte Radformen geeignet und dabei kostengünstig, leicht zerspanbar und
geräuschdämpfend. Die Tragfähigkeit ist gering.
Wenn Sie die Option „Eigene Eingabe“ auswählen, werden alle Eingabe- und Auswahlmöglichkeiten aktiviert und Sie können Ihren individuellen Werkstoff anlegen. Ihre Eingaben werden beim Speichern in eine Berechnungsdatei mitgespeichert. Wählen Sie allerdings im Modul einen anderen Werkstoff aus der Listbox aus, gehen Ihre definierten Angaben verloren. Diese müssen Sie anschließend erneut eingeben.
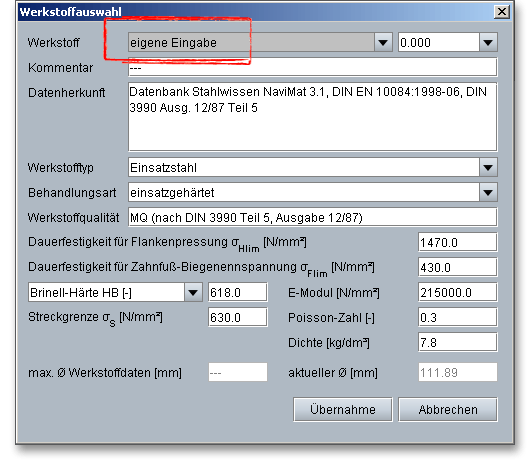
Die von außen auf ein Getriebe einwirkenden dynamischen Zusatzkräfte werden durch den Anwendungsfaktor \(K_{A}\) bestimmt. Diese Zusatzkräfte sind abhängig von den Eigenschaften der treibenden und der getriebenen Maschine, den Kupplungen, den Massen- sowie den Betriebsverhältnissen. Da Fressen kein Ermüdungsschaden ist, soll der Anwendungsfaktor bei der Fresstragfähigkeitsberechnung den stärkeren Einfluss einzelner hoher Lastspitzen berücksichtigen. Einzelne Lastspitzen beeinflussen direkt nur die Flankentemperatur. Deshalb kann für die Berechnung der Fresstragfähigkeit der gleiche Anwendungsfaktor \(K_{A}\) wie für die Grübchen- und Zahnfußtragfähigkeit verwendet werden. Die nachfolgende Tabelle zeigt Anhaltswerte für den Anwendungsfaktor:
| Arbeitsweise der | ||||
| Antriebsmaschine | gleichmäßig | mäßige Stöße | mittlere Stöße | starke Stöße |
| (uniform) | (moderate) | (heavy) | ||
| gleichmäßig (uniform) | 1,0 | 1,25 | 1,5 | 1,75 |
| leichte Stöße | 1,1 | 1,35 | 1,6 | 1,85 |
| mäßige Stöße (moderate) | 1,25 | 1,5 | 1,75 | 2,0 |
| starke Stöße (heavy) | 1,5 | 1,75 | 2,0 | 2,25 oder höher |
Hinweis: Neben dem Eingabefeld für den Anwendungsfaktor finden Sie einen Fragezeichen-Button. Klicken Sie dort, öffnet sich die obenstehende Tabelle. Einen solchen Fragezeichen-Button werden Sie noch häufiger neben verschiedenen Eingabefeldern finden.

Der Breitenfaktor \(K_{F\beta }\) für die Zahnfußbeanspruchung berücksichtigt den Einfluss der ungleichmäßigen Lastverteilung über den balligen Kegelradflanken. Für die Berechnung wird der Breitenfaktor \(K_{H\beta }\) für die Zahnflankenbeanspruchung genutzt. Mit dem eAssistant lässt sich der Breitenfaktor individuell eingeben oder nach ISO 10300 Teil 1 Methode C berechnen. Klicken Sie dazu auf den den Taschenrechner-Button, um die Eingabemaske zur Auslegung des Breitenfaktors zu öffnen.

In der Listbox ist bereits der Eintrag „ISO 10300 Teil 1 Methode C“ gewählt und das Eingabefeld für den Lagerungsfaktor \(K_{H\beta -be}\) aktiv. Die Tabelle bietet Ihnen Anhaltswerte für \(K_{H\beta -be}\). Geben Sie einen Wert aus dieser Tabelle in das Eingabefeld ein und klicken Sie auf den Button „Übernahme“. Der Breitenfaktor wird automatisch berechnet und anschließend in die Hauptmaske übernommen.
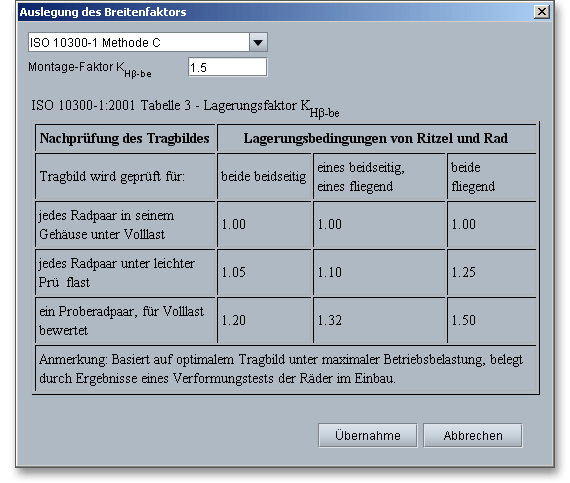
Die nachfolgende Tabelle zeigt Näherungswerte für den Lagerungsfaktor \(K_{H\beta -be}\):
| Nachprüfung des Tragbildes für | Lagerungsbedingungen von Ritzel und Rad
| ||
| beide beidseitig | eines beidseitig, | beide fliegend | |
| eines fliegend | |||
| jedes Radpaar in seinem Gehäuse unter Volllast | 1,00 | 1,00 | 1,00 |
| jedes Radpaar unter leichter Prüflast | 1,05 | 1,10 | 1,25 |
| ein Proberadpaar, für Volllast bewertet | 1,20 | 1,32 | 1,50 |
Arbeiten Sie mit einem bereits festgelegten Breitenfaktor, können Sie diesen im Modul eingeben. Klicken Sie in der Hauptmaske auf den Taschenrechner-Button. In dem Fenster zur Auslegung des Breitenfaktors wählen Sie aus der Listbox „eigene Eingabe“. Klicken Sie anschließend auf den Button „Übernahme“.
In der Hauptmaske ist jetzt das Eingabefeld für den Breitenfaktor aktiviert und Sie können Ihren individuellen Faktor eingeben. Wenn Sie diesen Breitenfaktor für mehrere Berechnungen benötigen, dann speichern Sie diesen als Standard-Vorlage. Somit öffnet sich das Berechnungsmodul immer mit dem definierten Breitenfaktor und Sie müssen den Wert nicht ständig neu eingeben.

Reibung und Verschleiß an den Zahnflanken sollen durch den Schmierstoff verringert werden, denn die Zahnflankenreibung ist beispielsweise für Flankenabnutzung, Getriebeerwärmung sowie für das Getriebegeräusch verantwortlich. Eine verminderte Zahnflankenreibung verbessert den Wirkungsgrad, der allerdings noch von der Zahnbelastung, der Umfangsgeschwindigkeit, der Verzahnungsqualität und der Oberflächenbeschaffenheit der Zahnflanken abhängt. Soll ein Getriebe einwandfrei arbeiten, so hängt dies doch wesentlich vom gewählten Schmierstoff ab. Hier bietet sich ein flüssiger Schmierstoff an, der leicht zwischen die Zahnflanken gebracht werden kann. Ein Schmierstoff hat aber auch die Aufgabe, Reibungswärme abzuführen und Getriebeelemente so vor Korrosion zu schützen. Meist werden auch die zum Getriebe gehörigen Lager und Kupplungen mit dem Schmierstoff versorgt, der somit auch dafür geeignet sein muss.

Für die Wahl flüssiger Schmierstoffe gilt im Allgemeinen: „Je kleiner die Umfangsgeschwindigkeit und je größer
die Wälzpressung sowie die Rauigkeit der Zahnflanken sind, um so höher muss die Viskosität sein.
Eine höhere Viskosität bewirkt eine größere hydrodynamische Tragfähigkeit und Belastbarkeit,
und somit auch eine höhere Fresslastgrenze, bei der Riefenbildung oder Fressen der Zahnflanken
einsetzt.“ (Muhs/Wittel/Jannasch/Voßiek: Roloff/Matek Maschinenlemente, 17. überarbeitete Auflage, Vieweg
Verlag, Wiesbaden 2005)
Hinweis: Die Viskosität eines Schmiermittels sollte hoch sein, wenn das Getriebe wechselnden Belastungen
ausgesetzt ist, da dadurch auftretende Stöße gedämpft werden.
Im Gehäuse laufende Räder werden fast ausnahmslos mit Öl geschmiert. Hierbei unterscheidet man zwischen
Tauch- und Einspritzschmierung.
Öl-Tauchschmierung: Die Öl-Tauchschmierung ist ein einfaches, zuverlässiges und kostengünstiges
Schmiersystem. Bei der Tauchschmierung tauchen die Zahnräder entweder selbst oder mit einem Hilfsrad in
eine Schmierstofffüllung ein, wobei das Öl direkt an die Zahnflanken gerät oder durch Abtropfen von den
Wänden auf die Zahnflanken gelangt. Die Öl-Tauchschmierung findet bei niedrigen bis mittleren
Geschwindigkeiten (bis etwa \(\nu \) = 20 m/s) Anwendung.
Öl-Einspritzschmierung: Bei der Öl-Einspritzschmierung kann man das Öl in seinem Kreislauf filtern, kühlen und
überwachen und auch den Lagern direkt Öl zuführen. Die Ölmenge lässt sich nach der abzuführenden
Wärmemenge dosieren. Als Ölbehälter dient das Getriebegehäuse oder ein außerhalb angeordneter Behälter,
aus dem mehrere Aggregate versorgt werden können. Das Öl wird mit Hilfe einer Pumpe über Düsen vor oder
unmittelbar in den Zahneingriff eingespritzt. Bei Umfangsgeschwindigkeiten von \(\nu \) > 20 m/s kommt die
Öl-Einsspritzschmierung zum Einsatz.
Fettschmierung: Die Wahl eines Fettes hängt von der Umfangsgeschwindigkeit, der Art des Auftrags und der
Gebrauchstemperatur ab. Eine Fettschmierung erfordert eine geringe Wartung und schützt gegen
Verschmutzung.
Wählen Sie den Schmierstoff direkt aus der Listbox aus oder klicken Sie auf den Button „Schmierstoff“, um in die umfangreiche Schmierstoffdatenbank zu gelangen.
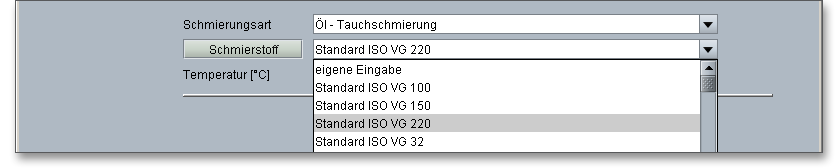
In der Schmierstoffdatenbank erhalten Sie detaillierte Informationen zu den Ölen und Fetten, wie zum Beispiel die Dichte, die Viskosität oder die Kraftstufe des FZG-Tests. Wählen Sie aus der Listbox „eigene Eingabe“, so lässt sich auch hier ein individueller Schmierstoff definieren.
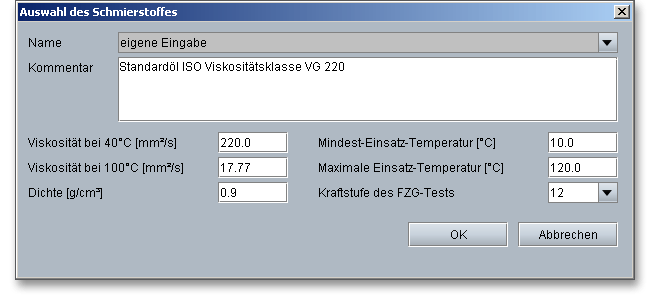
Klicken Sie in der Hauptmaske der Tragfähigkeit auf den Button „Fuß/Flanke“, so werden die erweiterten Eingabeoptionen aufgerufen.

Ändern Sie in der dann folgenden Maske keine Eingaben, so wird mit den Standard-Eingabewerten weiter gerechnet.
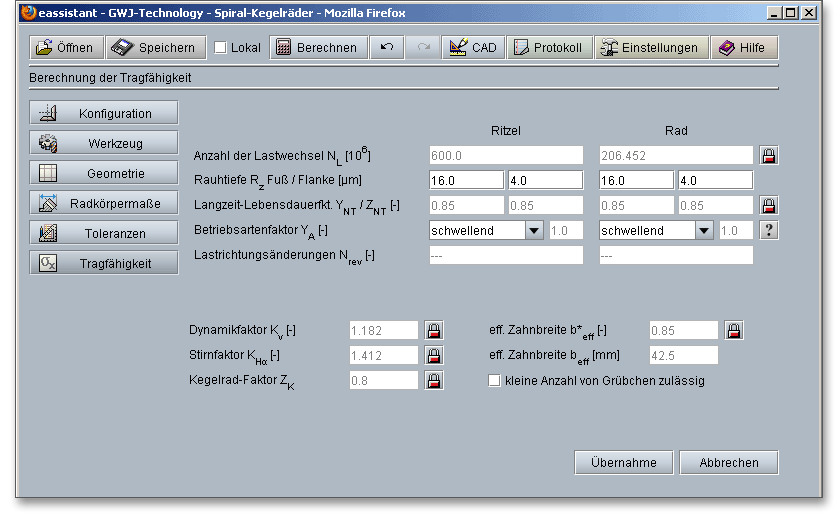
Die Oberflächenrauigkeit der Flanken beeinflusst die Flankentragfähigkeit. Die gemittelte Rautiefe \(R_{z}\) ist das arithmetische Mittel aus den Einzelrautiefen fünf aneinandergrenzender Einzelmessstrecken. Die Eingabe der Rautiefe erfolgt für Ritzel und Rad am Fuß und an der Flanke. Die Öberflächenrauigkeit eines Werkstückes wird hinsichtlich der zu erfüllenden Funktion und nach der wirtschaftlichen Fertigung gewählt. Hohe Herstellkosten ergeben sich aus einer zu feinen Oberfläche. Eine zu grobe Oberfläche kann unter Umständen nicht die geforderte Funktionalität erfüllen.

Der Lebensdauerfaktor \(Y_{NT}\) am Zahnfuß und der Lebensdauerfaktor \(Z_{NT}\) an der Flanke berücksichtigen die gegenüber
der Dauerfestigkeit höhere Zahnflanken- und höhere Zahnfußtragfähigkeit bei einer begrenzten Anzahl von
Lastwechseln. Die Faktoren werden hauptsächlich vom Werkstoff sowie der Wärmebehandlung
beeinflusst.
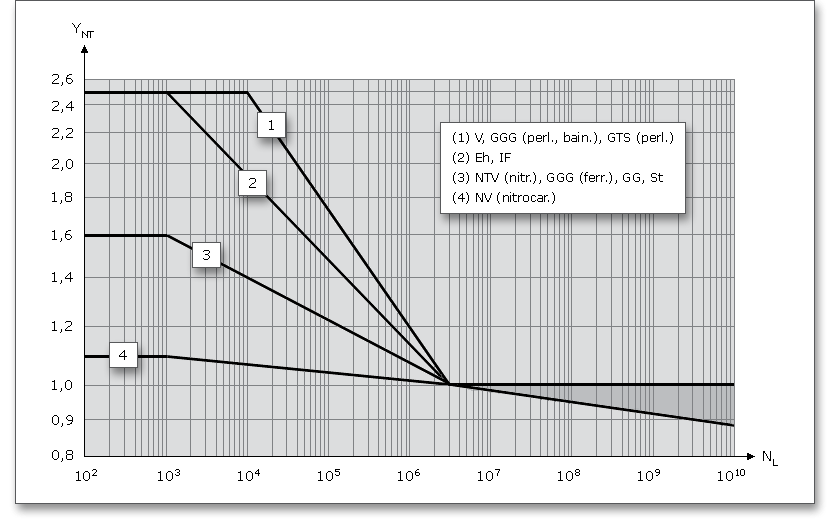
Lebendauerfaktor \(Y_{NT}\):
Für Lastwechselzahlen \(N_{L} > 3 \cdot 10^{6}\) kann bei optimalen Voraussetzungen von Werkstoff- und Herstellqualität mit \(Y_{NT}\) = 1
gerechnet werden. Im Bereich der statischen Beanspruchung, also \(N_{L} < 10^{3}\), wird der Lebensdauerfaktor zu
2,5.
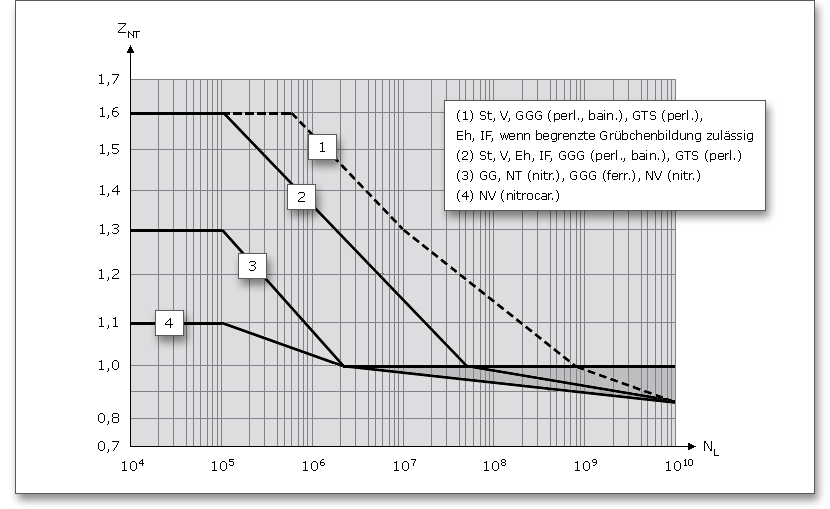
Lebensdauerfaktor \(Z_{NT}\):
Für Lastwechselzahlen \(N_{L} > 5 \cdot 10^7\) kann bei optimalen Voraussetzungen von Werkstoff- und Herstellqualität mit \(Z_{NT}\) = 1
gerechnet werden. Im Bereich der statischen Beanspruchung (\(N_{L} < 10^{3}\)) wird der Lebensdauerfaktor zu
1,6.
Mit Hilfe der grafischen Abbildung lässt sich \(Y_{NT}\) bzw. \(Z_{NT}\) für die statische Festigkeit und die Dauerfestigkeit abhängig von Werkstoff und Wärmebehandlung darstellen:
Die Faktoren lassen sich über den Schloss-Button individuell modifizieren. Klicken Sie auf den Schloss-Button,
dann werden die Eingabefelder aktiviert und die Lebensdauerfaktoren können angepasst werden. Denken Sie
daran, den Schloss-Button geöffnet zu lassen, sonst werden die ursprünglichen Standardwerte wieder
eingesetzt.
Die Zahnfuß-Dauerfestigkeit \(\sigma _{Flim}\) wird mit dem Einfluss der Betriebsart korrigiert.
\[\sigma _{Flim} = \sigma _{Flim0} Y_{A}\]
| \(\sigma _{Flim0}\) | Zahnfuß-Dauerfestigkeit aus Werkstoff-Kennwerten |
| \(\sigma _{Flim}\) | Zahnfuß-Dauerfestigkeit mit Einfluss des Betriebsartenfaktors |
| \(Y_{A}\) | Betriebsartenfaktor (siehe nachfolgende Tabelle) |
Für den Betriebsartenfaktor \(Y_{A}\) können die folgenden Anhaltswerte verwendet werden:
| Betriebsartenfaktor \(Y_{A}\) nach Linke8
| ||
| Betriebsart | Betriebsartenfaktor \(Y_{A}\) | Belastungsrichtung |
| schwellend | 1 |  |
| wechselnd | 0,7 | 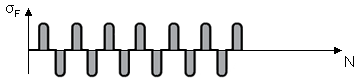 |
| reversierend | 0,85 - 0,15 \(\frac {lgN_{rev}}{6}\) (für \(1\leq N_{rev} \leq 10^{6}\)) 0,7 (für \(N_{rev} > 10^{6}\)) | 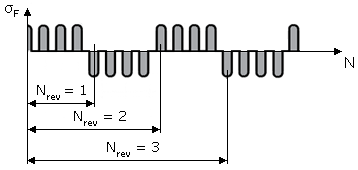 |
| Hinweis: \(N_{rev}\) = Anzahl der Lastrichtungsänderungen während der Betriebszeit
| ||
| 8 Tabelle aus: Linke, H.: Stirnradverzahnung Berechnung Werkstoffe Fertigung, Carl Hanser
Verlag München Wien, 1996, S. 321, Tab.: 6.5/7
| ||
Die Tabelle für den Betriebsartenfaktor lassen sich über den Fragezeichen-Button öffnen.

Der Dynamikfaktor \(K_{V}\) berücksichtigt innere dynamische Zusatzkräfte. Infolge von Flankenlinienabweichungen, Breitenballigkeit der Zahnflanken, Verformung der Zähne, des Gehäuses, der Wellen und der Radkörper sowie Schwingungen der Radmassen kommt es zu inneren dynamischen Zusatzkräften. Sie steigen mit der Umfangsgeschwindigkeit der Zahnkränze, nehmen aber mit steigender Belastung der Zähne ab. Der Dynamikfaktor kann über das Schloss-Symbol manuell eingegeben werden.

Die Stirnfaktoren berücksichtigen die Auswirkung ungleichmäßiger Kraftaufteilung auf mehrere gleichzeitig im
Eingriff befindliche Zahnpaare (das heißt in Umfangsrichtung) auf die Flankenpressung (\(K_{H\alpha }\)), auf die
Fressbeanspruchung (\(K_{B\alpha }\)) und auf die Zahnfußbeanspruchung (\(K_{F\alpha }\)). Der Stirnfaktor kann über das Schloss-Symbol
manuell eingegeben werden.
Der Kegelradfaktor \(Z_{K}\) berücksichtigt den Einfluss des von der Evolvente abweichenden Zahnprofils
auf die Grübchentragfähigkeit, insbesondere den positiven Einfluss der bei Kegelrädern üblichen
Höhenballigkeit. \(Z_{K}\) soll auch den Einfluss der über der Breite veränderlichen Zahnsteifigkeit erfassen. \(Z_{K}\) wurde
aufgrund von Prüfstandversuchen und Betriebserfahrungen mit ausgeführten Kegelradgetrieben
verschiedener Anwendungsgebiete abgeschätzt. Für die Kegelräder mit einer angepasster Höhenballigkeit
wird für \(Z_{K}\) = 0,8 gewählt. Der Kegelradfaktor kann über das Schloss-Symbol manuell eingegeben
werden.
\(b_{e}\)ist die effektive Zahnbreite (Tragbildbreite). Unter Volllast beträgt die Tragbildbreite mindestens 85% der Zahnbreite. Für den Fall, dass keine Informationen zu den Belastungen vorliegen, kann \(b_{e} = 0,85 \cdot b\) gesetzt werden. Klicken Sie auf das Schloss-Symbol, um den Faktor für die effektiv wirksame Zahnbreite einzugeben.

In einzelnen Fällen kann die Bildung von Grübchen an der Zahnflanke zugelassen werden. Hier finden Sie also die Option „Grübchen zulassen“. Anfänglich auftretende, zum Stillstand kommende Grübchenbildung ist im allgemeinen oft zulässig. Oft gehen insbesondere bei einsatzgehärteten oder nitrierten Verzahnungen von Grübchen in Zahnfußnähe Ermüdungsbrüche aus, wodurch eine jeweils individuelle Beurteilung erforderlich ist. In einigen Grenzfällen (Luft- und Raumfahrt) sind deshalb einzelne Grübchen absolut unzulässig. Auch bei Turbogetrieben können Grübchen zu Schwingungen und zu erhöhten dynamischen Zusatzkräften führen.

Das Berechnungsmodul enthält ein Meldungsfenster, in denen Informationen, Hinweise oder Warnungen aufgelistet werden. Der eAssistant erkennt bereits während der Dateneingabe auftretende Fehler und zeigt Ihnen sogleich Lösungsvorschläge im Meldungsfenster an. Wenn Sie die Hinweise beachten, lassen sich schnell Fehler in Ihrer Berechnung beheben. Die folgenden Meldungen können zum Beispiel auftreten:

Zusätzliche Informationen erhalten Sie auch über die Kurzhilfe. Bewegen Sie einfach den Mauszeiger über ein Eingabefeld oder über einen Button und Ihnen werden die Informationen in der Kurzhilfe angezeigt.

Die Ergebnisse werden bereits während jeder Eingabe berechnet und immer aktuell im Ergebnisfeld angezeigt. Es wird nach jeder abgeschlossenen Eingabe neu durchgerechnet. Dadurch werden jegliche Veränderungen der Eingabewerte auf die Ergebnisse schnell sichtbar.
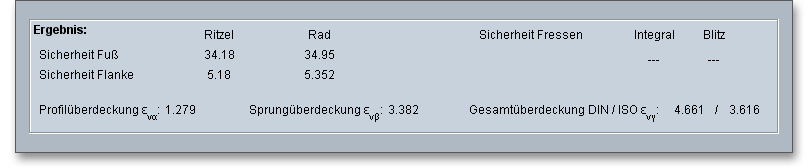
Werden die Mindestsicherheiten nicht erfüllt, so wird das Ergebnis mit einer roten Markierung angezeigt. Grundsätzlich können Sie jede Eingabe mit der Enter-Taste oder mit einem Klick in ein neues Eingabefeld abschließen. Alternativ können Sie mit der Tab-Taste durch die Eingabemaske springen oder nach jeder Eingabe auf den Button „Berechnen“ klicken. Auch hierbei werden die Eingabewerte entsprechend übernommen und die Ergebnisse sofort in der Übersicht angezeigt.
Nach Abschluss Ihrer Berechnung können Sie ein Protokoll erzeugen. Klicken Sie dazu auf den Button „Protokoll“.
Das Protokoll enthält ein Inhaltsverzeichnis. Hierüber lassen sich die gewünschten Ergebnisse schnell aufrufen. Es werden alle Eingaben sowie Ergebnisse aufgeführt. Das Protokoll steht Ihnen im HTML- und im PDF-Format zur Verfügung. Sie können das erzeugte Protokoll zum Beispiel im HTML-Format abspeichern, um es später in einem Web-Browser wieder oder im Word für Windows zu öffnen.
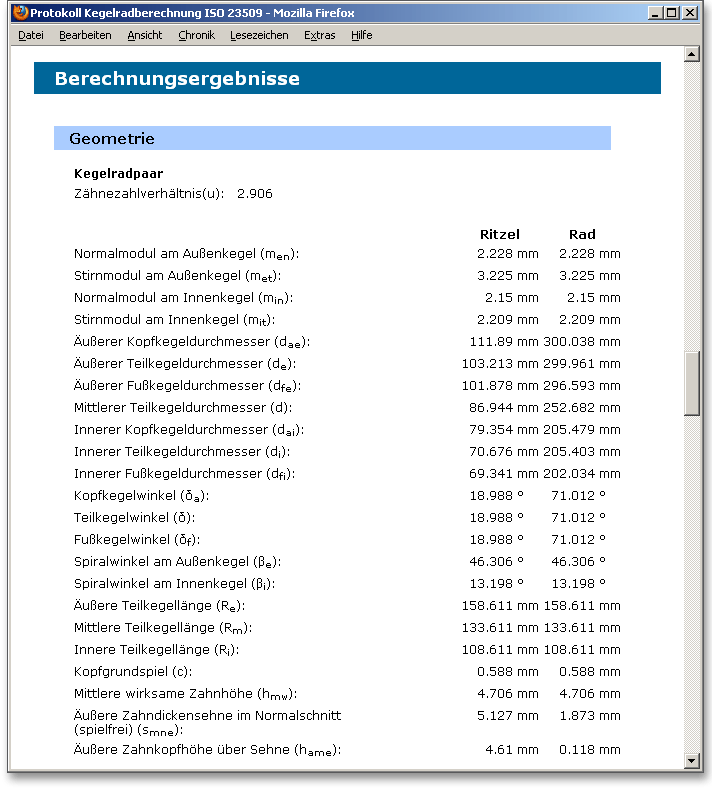
Das Berechnungsprotokoll lässt sich drucken oder speichern:
Nach der Durchführung Ihrer Berechnung können Sie diese speichern. Sie haben dabei die Möglichkeit, entweder auf dem eAssistant-Server oder auf Ihrem Rechner zu speichern. Klicken Sie auf den Button „Speichern“ in der obersten Zeile des Berechnungsmoduls.
Um die Berechnung lokal auf Ihrem Rechner zu speichern, müssen Sie die Option „Lokal“ im Berechnungsmodul aktivieren.
Haben Sie diese Option nicht aktiviert, so öffnet sich ein neues Fenster und Sie können Ihre Berechnung auf dem eAssistant-Server speichern. Geben Sie unter „Dateiname“ den Namen Ihrer Berechnung ein und klicken Sie auf den Button „Speichern“.
Mit dem Button „Zurück“ (linker Pfeil) können Sie vorhergegangene Eingaben zurücksetzen. Wenn Sie eine rückgängiggemachte Eingabe wiederherstellen wollen, dann klicken Sie auf den Button „Vorwärts“ (rechter Pfeil).
In der obersten Zeile des Berechnungsmoduls finden Sie den Button „CAD“.
Auf der Basis Ihrer Berechnung lassen sich über diesen Button „CAD“ und mit Hilfe des eAssistant CAD-PlugIns
Kegelräder in einem 3D-CAD-System, wie zum Beispiel SOLIDWORKS oder Solid Edge, erzeugen.
Auf Basis Ihrer Berechnung können mit dem eAssistant CAD-PlugIn spiralverzahnte Kegelräder featurebasiert im 3D automatisch erstellt werden. Toleranzen, Kopfkantenbruch, Profilverschiebung werden mit berücksichtigt und es wird die exakte Zahnform modelliert. Klicken Sie auf den Button „CAD“, anschließend wählen Sie das entsprechende CAD-System, zum Beispiel SOLIDWORKS oder Solid Edge, für den Export aus.
Öffnen Sie jetzt ein CAD-System. Über einen integrierten Menüpunkt „eAssistant“ im CAD-System können Sie
mit der Generierung der berechneten Kegelräder starten.
Hinweis: Das entsprechende eAssistant CAD-PlugIn muss bereits auf Ihrem CAD-Rechner installiert sein. Das
Plugin steht zum Download auf unserer Webseite www.eAssistant.eu bereit.
Zu den entsprechenden 2D-Ableitungen der Kegelräder können jederzeit per Mausklick auch die Herstelldaten
auf eine Zeichnung plaziert werden.
Hinweis: Benötigen Sie nähere Informationen zum eAssistant CAD-Plugin, so können Sie sich jederzeit gern
an uns wenden. Weitere Einzelheiten erfahren Sie auch über unsere Webseite www.eAssistant.eu oder in
dem Hilfe-Manual zum eAssistant CAD-PlugIn, welches Sie auch auf der Webseite finden können.
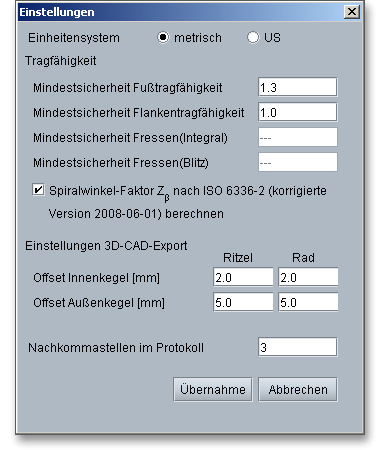
Klicken Sie auf den Button „Einstellungen“ in der obersten Zeile des Berechnungsmoduls, dann können Sie programmspezifische Optionen anpassen, zum Beispiel die Anzahl der im Protokoll angegebenen Nachkommastellen.
Diese Option gibt Ihnen die Möglichkeit, die folgenden Standardeinstellungen zu ändern: